Kusee's Blog: Chp05. 삼각비

2020년 4월 15일 수요일

Chp05. 삼각비

00.정의
직각삼각형에서 직각이 아닌 두 내각중 1개의 내각이 정해지면 나머지 1개의 내각이 정해지니까 1개의 내각이 정해진(삼각형에서 2개의 각을 아니까) 삼각형끼리는 “닮음이다”

01.삼각비의 뜻
=삼각비=직각삼각형에서 두 길이의 비
=(각)a의 삼각비 = (각)b=90’인 직각삼각형 ABC에서 대변의 길이를 abc라고 하면

**이때 sin a 에서 높이/빗변의 길이 에서 각의 위치에 따라 높이와 빗변의 위치가 달라지기 때문에 주의해야 한다**

02.1개의 삼각비만 주어질 때 삼각비
개념=사인,코사인 탄젠트 중 하나의 삼각비만 주어질 때 나머지 길이는 피타고라스의 정리로 구한다
Ex)sin a=3/5일 때 tan A , cos A 를 구하라

(선분)AB는 √5^2-3^2 = √25-9 = √16 = 4
Tan A = 3/4 , Cos A = 4/5

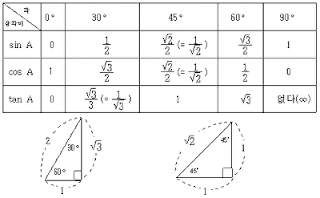
03.특수각의 삼각비
한 내각의 크기가 30,45,60인 직각삼각형의 비

**특수각을 잡는건 30,45,60으로 직각의 왼쪽부분의 각을 지정한다**

04.예각의 삼각비
정의=반지름의 길이가 1인 원에서 임의의 예각 x에 대한 비를 지칭하는것

0,90도 에서 삼각비는
0 90
Sin 0 1
Cos 1 0
Tan 0

05.삼각비의 표
정의=0에서 90사이의 각을 1’ 간격으로 나누어 삼각비의 근사값을 나타낸 것
방법=삼각비의 표에서 가로줄과 세로줄이 만나는 곳의 수가 삼각비의 근사값이다

06.직각삼각형의 변의 길이
(각)C=90’인 직각삼각형 ABC에서

(각)b의 크기와 빗변의 길이 c를 알 때
A= c cosB – c*a/c = a
B= c sinB

(각)b의 크기와 밑변길이 a를알 때
b=a Tan B , c=a/cosB

(각)B의 크기와 높이 B를 알 때
A=b/tanB C=b/sinB

06.일반 삼각형의 변의 길이
=길이를 구하고자 하는 변이 빗변인 직각 삼각형이 되도록 수선을 그어 주어진 삼각형을 2개의 직각삼각형으로 나눈다

=두변의 길이와 끼인각을 알 때

(삼각형)ABH에서 (선분)AH= C cosB
(선분)BH=C cosB 이므로 (선분)CH = (선분)BC - (선분)BM = a – c CosB
따라서 (선분)AC = √(선분)AH^2 + (선분)CH^2 = √(CsinB)^2+(a-CcosB)^2

=한변의 길이와 양 끝각의 크기를 알 때
수선으로 나누어진 두 직각 삼각형의 높이가 같음을 이용해 변의 길이를 구한다

07.삼각형의 높이
밑변의 길이와 양 끝각의 크기가 주어진 삼각형의 높이 h는 삼각비를 이용해 구할수 있다
==예각 삼각형의 높이