Chp06. 원의 성질

01.현의 수직 이등분선
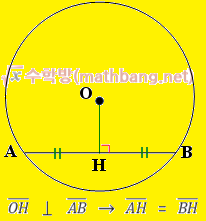
정의:원의 중심에서 현에 내린 수선은 해당 현을 이등분 한다

02.현의길이
=한원 또는 합동인 두원에서 원의 중심으로부터 같은 거리에 있는 두 현의 길이는 같다
=길이가 같은 두 현은 원의 중심으로부터 같은 거리에 있다

03.원의 접선의 길이

**원 밖의 한점에서 해당 원에 그린 두 선의 길이는 같다**



04.삼각형의 내접원
원o가 삼각형 ABC에 내접하고 내접원의 반지름이 R일 때
=원밖의 1점에서 그은 두 점선의 길이는 서로 같다

=ABC의 둘레의 길이는 a+b+c = 2(x+y+z)
=ABC의 넓이 = 1/2r(a+b+c)



05.외접 사각형의 성질
=원에 외접하는 사각형의 두 쌍의 대변의 길이의 합은 같다
=두쌍의 대변의 길이의 합이 서로 다른 사각형은 원에 외접한다

06.원주각과 중심각의 크기
원주각=원에서 호 ab를 제외한 원위에 한점 p가 있을 때 (각)apb를 (선분)ab에 대한 원주각이라고 한다

한원에서 한 호에 대한 원주각의 크기는 그 호에 대한 중김각 크기의 1/2이다 (각)APB= 1/2(각)AOB

07.원주각의 성질
한원에서 한 호에 대한 원구각의 크기는 모두 같다

반원에 대한 원주각의 크기는 90’ 이다

08.원주각의 크기와 호의 길이
한원 또는 합동인 두 원에서
=길이가 같은 호에 대한 원주각의 크기는 같다
=크기가 같은 원주각에 대한 호의 길이는 같다
=원주각의 크기와 호의 길이는 정비례 한다

09.4점이 한원위에 있을조건

두점 CD가 직선 AB에 대해 같은 곳에 있을 때 4점이 한원 위에 있다고 할수 있다



10.원에 내접하는 사각형의 성질

원에 내접하는 사각형의 한 외각의 크기는 이웃하지 않는 내각의 크기와 같다



11.접선과 현이 이루는각
정의:원의 접선과 그 접점을 지나는 현이 이루는 각의 크기는 각의 내부에 있는 호 (AB)에 대한 원주각 ACB와 같다

접선이 되기 위한 조건
원 O에서 (각)BAP = (각)BCA 이면 직선 AP는 원 O의 접선이다



12.두원에서 접선과 현이 이루는 각
두 원이 한점 T에서 만나면 두현 AC,BD는 평행한다