Chp15. 상관과 회귀

본론
"내라인은 무었일까?"
"변수들 사이에 존재하는 연결에 대해 , 상관(Correlation) 회귀(Regression)을 통한 분석"

데이터의 종류=Type
1.일변향 데이터(univarate data)
단일 변수의 도수와 확율에 관심을 가진다
ex)카지노에서 돈을 딸 확율, 사람들의 몸무게등

2.이변량 데이터(bivariate date)
하나가 아닌 두개의 변수값을 말해준다

3.독립(independent) 설명(explanatory) 변수
변수하나가 통제되거나 다른변수를 설명하는데 사용한다

4.종속(dependent)반응(response)
독립변수에 따라 바뀌는 변수

이변량 데이터의 시각화
하나의 값을 도수나 확율에 대입시키지 않고 x,y축에 대응시킨다
-->산포 다이어그램(sclatter diagram) 산정도(scatter plot)
독립변수 x축
종속변수 y축

"이때" x,y축이 만나는 점이 "직선" 형태라면 "선형(linear)"구조를 따른다 라고 한다

(좌측 상단 = 음수선형 , 좌측 하단 = 양수 선형 , 우측 하단=관계없음)

상관과 인과관계
두변수 사이에 상관이 있다고 해서 실세계에서도 상관이 있는지 확신할수 없다
--수학정 관련성이지 실세계의 연관이지 실세계 에서의 연관성이 아니다
ex)커피전문점이 증가하면 약국이 줄어든다는 패턴을 찾아도 실생활에서도 적용된다고 할수 없다

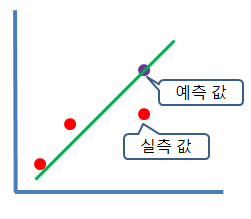
최적 적합선을 이용한 값의 예측
최량 적합선=Line of best fit - 산점도의 점들 사이를 관통하는 선을 하나 긋는것
주관적이며 분석자의 주관에 달려있다
어떻게 그려야 최선의 적합선일까?
직선을 나타내는 방정식을 찾는다
직선의 방정식 = y=a+bx

실측값과 예측값의 차이를 최대한 줄이는게 관건

제곱 오차의 합

실측값과 예측값에서 단순히 실측값-예측값을하면 값이 상쇄된다
**제곱연한이루에 더해야 한다**
이를 제곱 오차의 합이라고 한다
**Sum of squared errors**
SSE=Σ(y-^y)^2
y=a+bx에 기초한 SSE를 최소로 만드는 A,B를 찾아야 한다

b=Σ((x-_x)(y-_y)) / Σ(x-_x)^2

ex)
x 1.9 2.5 3.2 3.8 4.7 5.5 5.9 7.2
y 22 33 30 43 38 49 42 55

_x=34.7/8=4.4475
_y=311/8=38.875
Σ((x-_x)(y-_y))=122.53
Σ(x-_x)^2=23.02
b=122.53/23.02=5.32
y=a+5.32x


a구하기
_y=a+bx에서 a는
ex)_y=38.875 , _x=4.3375 b=5.32
a=38.875 - 5.32(4.3375) = 15.80
y=15.80+5.32x


-----------------------------------------
모집단이 아니라 표현에 대한것
b는 음수,양수 모두 해당
상관이 존재하지 않는 경우에도 최량적합선을 구할수있다

-->여기에 선을 그어도 의미가 없다
------------------------------------------

상관관계 확인

정확환 선형상관(회귀선과 데이터가 같은 양상
비선형 상관 - 회귀선과 데이터가 맞지 않는다

상관 계수(Correlation Coeftcient)
직선이 얼마나 잘 맞는지 계산한다
-1부터 1까지의 수로 측정 , r로 표시한다

좌측부터 r=-1 , r=0 , r=1
음수선형 , 약한선형 , 강한 선형 관계

R구하기
r=bSx/Sy
b=y=a+bx의 기울기 bSx/Sy
**b=Σ((x-_x)(y-_y)) / Σ(x-_x)^2**

Sx=x의 표준편차
**Sx=√Σ(x-_x)^2/n-1
Sy=y의 표준편차
**Sy=√Σ(y-_y)^2/n-1
ex)
x 1.9 2.5 3.2 3.8 4.7 5.5 5.9 7.2
y 22 33 30 42 38 49 42 55
b=5.32
Sx=√Σ(x-_x)^2/n-1 = √23.02/7 = √3.28857 = 1.81
Sy=√Σ(y-_y)^2/n-1 = √780.875/7 = √111.55357 = 10.56
r=5.32*1.81/10.56 = 9.6292/10.56=0.911

0.911 로 1에 가까운 상관계수를 가진다고 볼수있다