Chp8. 도형의 닮음

00.도형의 닮음
정의
=한 도형을 일정한 비율로 확대 축소하여 얻은 도형이 다른 도형과 합동이 될 때 닮음이라 한다, 이떄 대응하는 변의 길이를 닮은비 라고 한다

닮음의 조건
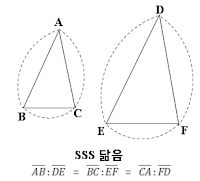
1.대응하는 세 쌍의 변의 길이의 비가 같을 때
2.대응하는 두쌍의 변의 길이의 비가 같고 끼인각의 크기가 같을 때
3.대응하는 두 쌍의 크기가 각각 같을 때



01. 닮은 도형
정의
=한 도형을 일정 비율로 확대 축소한 도형이 다른 도형과 합동이 될 때
작성법
=작성하는 꼭지점의 순서는 대응하는 순서로 작성한다
=(삼각형)abc와 (삼각형)def가 닮은 관계일 때 ~ (Similarity 의 s를 눕힌 표현)을 사용한다



02.닮음의 성질
평면 도형에서의 닮음의 성질
==대응하는 변의 길이비는 일정하다
==대응하는 각의 크기는 서로 같다
입체 도형에서의 닮음의 성질
==대응하는 모서리의 비는 일정
==대응하는 면은 복잡하다


03.삼각형의 닮음조건

 

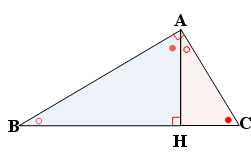
04.직사각형의 닮음
(각)A=90’ 인 직각 삼각형 abc에서 (선분)AHㅗ(선분)BC일 때 직각삼각형의 닮음관계
(삼각형)abc ~ (삼각형)hba ~ (삼각형)hac

05.삼각형에서 평행선과 선분의 길이의 비
(삼각형)abc에서 점 de가 (선분)ABㅗ(선분)AC의 연장선에 있을 때

06.삼각형의 내각의 이등분선의 성질
(삼각형)ABC 에서 (각)A의 이등분선이 BC와 만나는 점을 D라 하면

 

(선분)AB : (선분)AC = (선분)BD : (선분)DC
A의 연장선을 그으면
AE=AC
AB:AC=BD:CD


07.삼각형의 외각의 이등분선의 성질
(삼각형)ABC에서 (각)A 의 외각의 이들분선이 BC의 연장선과 만나는 점을 D라 하면

08.평행선 사이의 선분의 길이의 비
3개의 평행선이 다른 두 직선과 만날 때 평핼선 사이의 선분의 길이의 비와 같다

09.사다리꼴의 평행선과 선분의 길이의 비

10.평행선 사이의 선분의 길이의비 응용

AC와 BD의 교점이 E이고 AB // ef // DC 일때
BF : FC = BF : ED , AE:EC , AB:DC, 6:12
(삼각형)BCD에서 ED:CD = BE:BD=BE : (BE+ED)



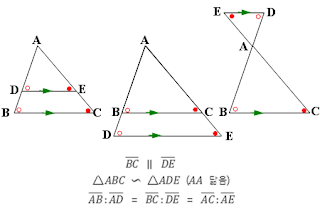
11.삼각형의 두 정점을 연결한 선분의 특징
특징:두 변의 중점끼리 연결한 선분은 나머지 변과 평행이고 길이는 남은 변의 1/2이다

12.사다리꼴의 중점을 연결한 선분의 성질

13.삼각형의 중선과 무게중심
중선
=삼각형의 한 꼭지점과 대변의 중선을 이은 선
무게중심
=세 중선의 길이를 각 꼭지점으로부터 2:1로 나눈다, 즉 ABC의 중심이 G일 때 AG : GD = BG : GE = CG : GF = 2:1

14.삼각형의 무게중심과 넒이
삼각형의 중선
==삼각형의 넓이를 이등분한다
삼각형의 무게중심과 넒이, 감각형의 세 중선에 의해 나누어지는 6개의 삼각형의 넓이는 모두 같다



15.평행사변형과 삼각형의 무게중심

16.닮은 도형의 넓이의 비와 부피의 비
넒이비 = 닮은비가 m:n이면 넓이비는 m^2 : n^2
부피비 = m^3 : n^3


17.닮음의 활용
축도:도형을 일정 비율로 줄여서 그린 그림
축척:축도에서 실제 도형을 줄인 비율
축도에서 실이와 실제 길이의 관계 = 축척 : 축도에서의 길이/실제길이
축도에서 길이 = 실제길이 * 축척
실제길이 = 축도에서의 길이/축척