Chp2. 중심적 경향 측정

본론
"데이터를 평균,중앙,최빈 등의 값을 구하고 데이터의 간결한 정리를 가능하게 한다"

평균(average)을 구하는 일반적 방법
평균값(mean)값 구하기

수학에서의 평균값
각각의 숫자를 문자로 표현해서 일반화 시키기
10,20,30,40,50 을 x1,x2,x3,x4 등으로 표현

모르는 수의 처리, 합
x1,x2,x3,x4...,xn의 총합
Σx= sigma 로 모든걸 더하게한다
평균값 수식 Σx/n 모든 수를 더하고 총 개수로 나눈다

평균값(mean)
μ(mu, 뮤)
μ=Σx/n 모든 수를 더하고 총 개수로 나눈다

도수 다루기
도수에서 똑같은 값이 반복될때 f문자가 있으면 곱해서 계산하기
μ=Σfx/Σf

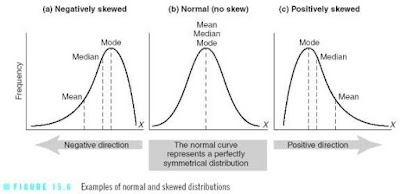
이상치(outlier)
다른 데이터에 비해 눈에 띄게 높거나 낮은값

편향된 데이터
이상치 내의 데이터가 그래프를 좌, 우측으로 잡아 끌어서 그래프의 모양이 바뀐다

**outlier 값이 우측, 이상적 데이터 분포, 좌측 분포**

중앙값
데이터에서 이상치를 피라시 위해 나열한 값의 가장 가운데 값들

*만약 데이터의 개수가 짝수라면 중앙값은?*
가운데 두수의 평균을 중앙값으로 사용

중앙값이 평균치보다 좋은가?
대부분의 경우 평균이 좋으며 특히 데이터의 표본 추출에서 안정적임

ex)
값 1 2 3 4 5 6 7 8
도수 4 6 4 4 3 2 1 1
Total = 25개
중앙값(mean) = 3
평균(avg) = 3

평균가 중앙값의 차이
평균과 중앙값이 같아도 데이터상에 존재하지 않을수 있다
값 1 2 3 31 32 33
도수 3 4 2 2 4 3
평균,중앙값이 모두 17이나 data 상에는 17이 없음

최빈값(mode)
도수 table에서 가장 자주 발생하는 수
수치 data 뿐만 아니라 범주 data에도 사용할수 있다

최빈값 구하기 3단계
1. 서로 구별되는 범주나 값 탐색
2. 값이나 범주의 도수 체크
3. 도수가 높은것 선택